Hello everyone! Welcome back to my blog series on Pascal’s Triangle. Today we will be looking at the first pattern covered in the last blog–triangular numbers, and their relation to the Hockey Stick Principle.
A short proof
To begin this blog, we will first prove the property of the triangular numbers shown in part 1:
What we want to prove
We want to prove that the numbers in the third diagonal of Pascal’s triangle are the triangular numbers. But that is hard to prove because of the non-rigor of the statement. So we need a definition:
Definition 2.1
The nth row of Pascal’s triangle is defined as the row with n+1 entries (Note: Yes, this does mean that the 0th row of Pascal’s triangle is actually the first row, but it will be more convenient later on to label it the way I have here), and we will call the nth entry in that row the n-1th number in the row (This is so the entries go from the 0th to the nth). Finally, the nth entry in the mth row of Pascal’s triangle will be labled mPn (Sorry for the weird notation here, the program I am writing this blog with doesn’t support making a subscript and superscript on the same character).
Now we can rewrite what we want to prove!
Theorem 2.1
Let Tn be the nth triangular number, defined as:
Tn=1+2+3+4+…+(n-1)+n
Then, Tn=(n+1)P(n-1)
Quick Interpretation
The most confusing part of the theorem is the (n+1)P(n-1) part, so let’s dissect it. What happens when n=1? We get (1+1)P(1-1)=2P0. If we look at where this is on Pascal’s triangle, we see it is on diagonal 3. This works for every n you can think of, so (n+1)P(n-1) is just another way to say diagonal 2. (Note: From now on, I will refer to diagonals starting from 0, so diagonal 3 I will now refer to as diagonal 2 as I did here, and same for all the other diagonals)
Proof
Now we can get to the proof! To start, we rewrite the definition of a triangular number recursively, as well as write the defining rule of Pascal’s triangle. First, the recursive definition of Tn:
Tn=n+Tn-1
This is true because of the natural repetition in the normal definition. Now, the defining rule for Pascal’s triangle:
nPm=n-1Pm+n-1Pm-1
This comes from the way we add numbers in Pascal’s triangle. Another thing to note is that the 0th diagonal numbers are always 1, i.e.
nP0=1=nPn
Now we are ready to begin. For this proof we will be using induction. Here’s a link to a website explaining it if you don’t know what it is already.
Base Case: n=1
In this case, we are proving 2P0=1. This is true by the property that 0th diagonal numbers are always 1.
Induction step: n=k –> n=k+1
Assume n=k works. Then, we have:
k+1Pk-1=Tk
We also have that:
k+1Pk=kPk+kPk-1=kPk+k-1Pk-1+k-1Pk-2= …
=kPk+k-1Pk-1+k-2Pk-2+…+0P0=k+1
Now, we have:
k+2Pk=k+1Pk+k+1Pk-1=Tk+k+1=Tk+1
And we are done!
Recap and Further Patterns
To recap, we just proved the first property from the last blog. Now, like I promised, I will show a principle which expands on this pattern known as the Hockey Stick Principle. Here is a picture explaining it:
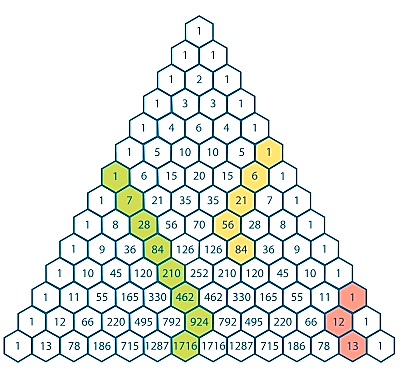
The idea is that the first numbers end up adding to the last number, so in the yellow Hockey Stick, 1+6+21+56=84. We will not prove this today, but it will lead our discussion of tetrahedral numbers and beyond in the next blog.
Good job! some typos:
1. In Definition 2.1, “we will call the nth entry in that row is the n-1th number in the row.” I guess you mean n-th entry is the (n+1)-th number.
2. Two typos at the end of the proof,
k+1Pk=kPk+kPk-1=kPk+k-1Pk-1+k-1Pk-2= …
=kPk+k-1Pk-1+k-2Pk-2+…+0P0=”k+1″ , and then k+2Pk=k+1Pk+k+1Pk-1=T_k+”k+1″=T_(k+1).
Fixed!
Why did you do the subscript superscript on the permutation notation? Couldn’t you just write mPn?
I tried, it just looked awkward when I did it. Wish they had a specialized equation block.
Actually, there is an equation block. If you write
\({^m}P_n\), it will actually show an equation (it just doesn’t work in the comment section). That is because MathJax uses Latex.Here is an image I created (in Discord, by the way) which has this.
I did not know this, thank you! I will be sure to use this in my future blogs.