Austrian physicist Erwin Schrödinger is one of the founders of quantum mechanics. In 1935, he posed this problem: imagine you take a cat and place it in a sealed box along with a radioactive device that had a 50% chance of killing the cat in the next hour. At the end of the hour, is the cat dead or alive? Common sense suggests that the cat is either dead or alive. But Schrödinger says that with quantum mechanics, the cat is both dead and alive. Only when the box is opened do we see a single definite state. Schrödinger did not try this project and see for himself; he just dismissed it as being “nonsensical” that he abandoned the theory he had once made, and instead pursued biology.
Now let us see what the Schrödinger equation is. This is the Schrödinger equation. $$E\Psi(x)=\dfrac{\hbar^2}{2m} \dfrac{d^2\Psi(x)}{dx^2}+V\Psi(x)$$
You might be thinking, “wait what is the Schrödinger equation?” I will explain. It is the quantum equivalent of a function you already know: Newton’s Second Law of Motion or \(F=ma\).
Say a ball weighs 120g and has an acceleration of 9.8 m/s2. Then its force will be 120g * 9.8 m/s2 or 1.2 N. If you also know some basic calculus, you can derive its position and momentum for any moment in time. And if you derive the position and momentum of the ball, you can derive things like velocity, kinetic energy, and so on. But if you go down to quantum-electron-particle-land, The Second Law of Motion does not work due to the Heisenberg Uncertainty Principle, which states that you cannot know the exact position and momentum of an electron. BUT!! We can know other things such as the wave function. But the wave function is hidden inside the Schrödinger equation!
“A-ha!”
Now let us go more in-depth about the Schrödinger equation (specifically, the time-independent version). So first let us put an electron in a box.

Now, let us say what we can know about the electron and where we can find them. Like, the energy levels and the position, etc. We can see them in the Schrödinger equation.
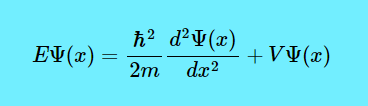
Let us start with this character: Ψ. This is the Greek letter Psi and it stands for the so-called “wave function”. It will tell you where the electron is likely to be.
But, electrons are sneaky in that you cannot predict where they will certainly be. We can only estimate where they will probably be.
The wave function gives a quantum-electro-probability of where the electron is likely to be.
BUT!! The electron can be in a superposition of all possible states at the same time. It is like Schrödinger’s Cat who is in a superposition of being dead and alive until the box is opened. It’s the same case here! The act of not knowing where the electron is means that the probability distribution of the electron’s position can be spread out over a wave-like space. Different waves can represent different probabilities of positions hence the name “wave function”. (And if you open the box, the wave function collapses.)
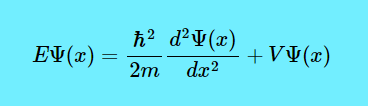
Now let us look at the letter E before the first Ψ. It means the energy levels of the electron. (By the way, this is an LHS = RHS equation, which means if you solve \(\dfrac{\hbar^2}{2m} \dfrac{d^2\Psi(x)}{dx^2}+V\Psi(x)\), you get the value of \(E\Psi(x)\).)
Now, note that there are some disallowed energy levels. If the electron is inside the box, there is a 0% chance that it is outside the box. So the wave function needs to be zero on both edges. If it is not zero, then there must be some probability that it will be outside the box, so the frequency will be considered disallowed. So Einstein discovered that the electron energy (\(E\)) is proportional to frequency (\(v\)) in the famous equation \(E=hv\) where \(h\) is Planck’s constant, or 6.62×10−34 J⋅Hz−1. So if certain frequencies are allowed in the box, and \(h\) is a constant, then it follows that only certain energy levels are allowed in the box. (And by the way, \(\hbar\) is equal to \(\dfrac{h}{2\pi}\), or the reduced Planck’s constant.)
Now let us figure out the RHS. Look at the equation \(E=KE+PE\) where E is the Overall Energy, KE is the Kinetic Energy and PE is the Potential Energy. If you skateboard on a skate ramp, while you are travelling across the “valley” then you will have KE. But when you arrive back at the top, the KE has transformed into PE. And even though you can switch back and forth between KE and PE, the total energy (KE+PE) is the same. Sometimes, Potential Energy is written as \(V\), like \(V\Psi(x)\).
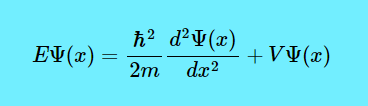
And if \(V\Psi(x)\) is the PE, then \(\dfrac{\hbar^2}{2m} \dfrac{d^2\Psi(x)}{dx^2}\) will be the KE. I know, the KE equation you are picturing in your mind is \(\dfrac{mv^2}{2}\) or \(\dfrac{1}{2} mv^2\), but the KE formula in the Schrödinger equation has a very complex derivation. So all the Schrödinger equation is saying is that if you know the KE and PE of a quantum system, then you know the allowed energy levels (E).
And there you have it. That is a brief intro to the Schrödinger equation. And, to finish off this blog, tell me whether or not this blog exists. Does it exist, does it not exist, or is it in a superposition? Open till the end of July.
Does the post exist?
This poll has been finished and no longer available to vote !
I Have Not Read A Post Like That Before… Its Truely Great…
Thank you!
Superb…after 23 years since introduced to the concept, I understood better with clarity
Thank you so much, Siddhivinayak Uncle! That means a lot!
At this age to know about undergraduate introductory course is simply GENIUS. Loved your understanding towards quantum mechanics.
Thank you!
This is simply superb! God bless you in abundance.
Thank you!
Excellent Atharv
Thank you!
As I read your precious blog, I’ll admit I didn’t understand anything… But feeling the freshly generated sympathetic resonance of the Primary cosmic wave emitting the spirit of your inspired writing…I can safely assume I have remembered everything!
Thank you for the ancient memory from the Akashic records!
Hey Atharv, loved the way you have articulated your thoughts. We will love to have a live on youtube at Cheenta Academy. Keep up this great work. You inspire us 😀
Thank you. It would be my pleasure to be there. Please WhatsApp the Meet link to my father.