Hello mathematicians! Today we are going to talk about \(\pi\) (aka Pi).
The discoverer of Pi is also the man who famously sat in a bathtub and discovered that the water level went up when he got in to the tub. Archimedes of Syracuse (287 BC – 212 BC) was an Italian-Greek mathematician, and he had come up with an approximation for Pi. We know that \(\pi = \dfrac{\text{Circumference}}{\text{Diameter}}\), but to get Pi, we need to measure a curved surface (the circumference). But Archimedes thought of it another way: a circle is actually a regular polygon, but it has an infinite number of sides and every side is infinitely small. Hence, the circle looks round.
Archimedes used what we now know as the “Method of Exhaustion”. Draw a square with its corners touching the circle (which I will call square A), and another square with its faces touching the circle (which I will call square B). The “diameter” of square A is the length of its diagonal (\(\sqrt{2}\) times the length of its side), and the “diameter” of square B is the length of its side. To get two estimates for Pi, which the actual value is in between, you should divide the perimeter of the square (4 times the length of the side) by its diameter. So you should get something like this:
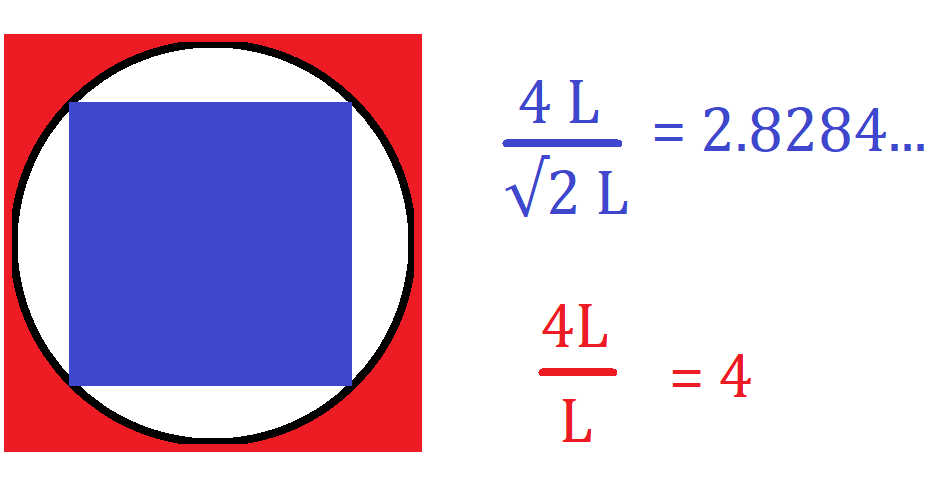
OK. So a square does not look more like a circle than a pentagon. And a pentagon does not look more like a circle than a hexagon. So you might say, “Does that mean, that when you increase the number of sides of the polygon, your estimates will become accurate?” I would say yes, and Archimedes thought so too1. Archimedes went up to a 96-gon (aka an enneacontahexagon or enneacontakaihexagon), and proved that \(\dfrac{223}{71} < \pi < \dfrac{22}{7}\), which, when translated to decimals (3.1408 < \(\pi\) < 3.1429), says that Archimedes found the value of Pi to 2 decimal places. But wait. Just 2 places?!
Yes, you say, you can do it better. What I did not tell you is that the Ancient Egyptians and the Babylonians estimated Pi more than a millenium before Archimedes. The Babylonian estimate of Pi was \(\dfrac{25}{8} = 3.125\). In the Ancient Egyptian Rhind Papyrus, they gave the value of Pi to be \(\dfrac{256}{81}\approx3.16\). There is also a famous Biblical estimate of Pi, which says Pi is 3:
And he made a molten sea, ten cubits from the one rim to the other it was round all about, and a line of thirty cubits did compass it round about.
– I Kings, 7:23
Back to Archimedes. In 212 BC, invaders of his hometown Syracuse, Italy killed him, and he was performing this calculation at this time. His last words were allegedly “μή μου τοὺς κύκλους τάραττε!” (Don’t disturb my circles!). European progress in Pi died with Archimedes. But a lot of the world was not in Europe, and mathematicians here were also interested in Pi. More specifically, Chinese, Indian, and Persian mathematicians were also interested in Pi. Chinese mathematicians used a very similar “Method of Exhaustion” to Archimedes, but instead of considering the shapes’ perimeters (what Archimedes did), they considered their areas (what Archimedes did not do). 3rd century Chinese mathematician Liu Hui (225 AD – 295 AD) used a polygon with \(3\times{2^{10}}=3072\) sides and measured Pi up to 4 decimal places now. Yes. Just 4. Not a big leap from Archimedes. 200 years later, mathematician Zu Chongzhi (429 AD – 500 AD) used a polygon with \(3\times{2^{12}}=12288\) sides to measure Pi to 5 decimal places. Still not a big leap from Archimedes and Liu Hui. This is a world record that stood for 800 years. But it was awkward just to do the calculation. A problem that would be resolved with the introduction of 2 revolutionary ideas: decimal notation and algebra.
Let us say that you and your friend together are 90 years old, and you are 35 years old. The question is, how old is your friend? You would usually write it as \(x+35=90\) where \(x\) is your friend’s age. You subtract 35 from both sides, and you get the answer: \(x=55\). Here I used two revolutionary ideas to the classical world. First, I wrote 90 and 35 using a simple notation. I can write any number using just 10 digits, and a place value system, where the position of a number determines its value. I also used 0 as a placeholder. For example, 87 is eighty-seven, but 807 is eight hundred and seven. So, to differentiate 87 and 807, I used a placeholder. Decimal notation was invented in India, and rapidly spread to Persia, where the next idea was invented. Secondly, I wrote my friend’s age using a symbol \(x\), and I changed both sides of the equation. This, of course, is algebra. This was invented technically by Babylonian and Ancient Greek mathematicians, but established by Persian mathematician Muḥammad ibn (sic) Mūsā al-Khwārizmī. After the Renaissance, Europe was back in the game! In 1630, Austrian astronomer and mathematician Christoph Grienberger. He used a \(10^{40}=10000000000000000000000000000000000000000\)-gon (really) to compute Pi to 38 decimal places, thus making it the most accurate estimate of Pi using the Method of Exhaustion. Yes. Still just 38. Compare it to the current record of 50 trillion decimal places. But can you draw a 10000000000000000000000000000000000000000-gon? No! The Method of Exhaustion lives up to its name, and makes you exhausted! Next up, the Infinite Revolution! Yes, you heard me right, the Infinite Revolution. This was a time period where mathematicians were moving away from the Method of Exhaustion, and shifting to a method based on infinite series. But, let us talk about infinite series.
There are two types of series: finite and infinite. Finite series actually stop at a finite amount:
\[3x+4x+5x+6x=18x\]
Infinite series, on the other hand, can converge or diverge. Convergent infinite series, for example, include the sum of non-zero non-negative powers of \(\dfrac{1}{2}\):
\[\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots=1\]
We can also write infinite series like this:
\[\sum_{k=1}^{\infty} \dfrac{1}{2^k}=1\]
Divergent series, on the other hand, is a series that goes to infinity. One obvious example is the sum of all square numbers:
\[\sum_{k=1}^{\infty} k^2=\infty\]
Let us go back to India, 3 centuries before Christopher Grienberger’s “most accurate value of Pi calculated using the Method of Exhaustion”. Madhava of Sangamagrama (1340 – 1425) created infinite series for the sine, cosine, tangent, and inverse tangent/arc tangent functions.
Quick refresher: If \(\tan{\theta}=\gamma\), then \(\tan^{-1}{\gamma}=\theta\). Get it? This also works for sine and cosine functions, but today we are going to focus only on the inverse tangent function.
If you “plug in” 1 into the inverse tangent function, the result is \(\dfrac{\pi}{4}\). (As long as you are using radians, because if you are using degrees, the result will be 45.) That brings us to the famous equation: \[\dfrac{\pi}{4}=1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\cdots\] Using this method, Madhava found the value of Pi till 10 decimal places. Madhava’s method seems to have been forgotten about until rediscovery by German polymath Gottfried Wilhelm Leibniz (1646 – 1716) and Scottish mathematician James Gregory (1638 – 1675). The first big Pi milestone or “Pilestone” was 100 digits (yes, including the 3), calculated by English astronomy professor John Machin (1686 – 1751) in 1706. Coincidentally, Welsh mathematician William Jones (1675 – 1749) also became the first person to use \(\pi\) as a symbol for Pi in 1706. The Pi calculation “industry” was turning more into a competition. That is because not all mathematicians were using the infinite series introduced by Madhava of Sangamagrama. They were using different infinite series which all converged on Pi. Some mathematicians were using the Wallis Product for Pi, introduced by English mathematician John Wallis: \[\dfrac{2}{1}\dfrac{2}{3}\dfrac{4}{3}\dfrac{4}{5}\cdots\] The current infinite series of choice was developed by Srinivasa Ramanujan (1887 – 1920): \[\dfrac{1}{\pi}=\dfrac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\dfrac{(4k)!(1103+26390k)}{k!^4(396^4k)}\] After Ramanujan’s passing, mechanical computers were used instead of actual infinite series. In 1949, American mathematicians (?) Levi B. Smith (birth and death dates unrecorded) and John Wrench (1911 – 2009) calculated Pi to 1119 decimal places, but their record was overtaken in the same year by the ENIAC, the first electronic computer programmed to compute Pi, nearly doubling their “world record” to 2036 decimal places. Now 2036 might sound like a lot, but you may not believe me if I say this: as of the time I am typing these very words on my computer, the world record for number of digits of Pi calculated belongs to Timothy Mullican. In 9 months and 30 days, he found the value of Pi up to \(50\times10^{12}=5000000000000\) decimal places. And still, it is just a piece of Pi.
Bye mathematicians, have fun, have a nice day, and I will see you next time!
And if you want to be in touch with me, please follow me on Instagram or subscribe to me on YouTube.
Well done! I liked the combination of math history, and actual equations!
Thank you Lucas!