Hello! Welcome to the next blog of the series! Today, we will be looking at inverses in modular arithmetic, and pose an interesting question whose solution will be part 4. Get ready, because we’re just about to learn about multiplication tables! Oh, and here are the last 3 blogs of the series!
Inverses in modular arithmetic
Additive
We all know that the negative numbers are the additive inverses of the positive numbers, i.e. -a is the additive inverse of a. This means that when we add -a and a, we get the additive identity. What is the additive identity? Well in a number system, the additive identity is the number i, such that:
i+a=a
For all a in said number system. Look familiar? It should! The additive identity of the real and natural numbers is 0! So when we say a is the additive inverse of b, we really mean that:
a+b=0
In modular arithmetic
In modular arithmetic, 0 is still clearly the additive identity. So, if we took a mod, say 5, and tried to find the additive inverse of 3, what would we get? Well clearly -3 works, but what else? We can be more clever, and say that since 3+2=5 which is 0 mod 5, that 2 is the additive inverse of 3. We can extend this to a general mod m, and say that the additive inverse of a, is m-a. This is a bit boring, and way too easy, so lets do something a bit harder and a way more fun!
Multiplicative
What about for multiplication? Well like before, a is a multiplicative inverse of b, if when we multiply a and b, we get the multiplicative identity. And just like before, the multiplicative identity is the number i, such that:
ia=a
For all a. This is, of course, 1. So, when we say a is the multiplicative inverse of b, we mean:
ab=1
In modular arithmetic
And this is where the focus of today’s blog lies, in multiplicative inverses in modular arithmetic. To start, the multiplicative identity in modular arithmetic is always 1. So now, lets try to find the multiplicative inverse of, lets say 4, in mod 12! Notice something? There isn’t an inverse! Try it for yourself, whatever you do, you can’t have 4*a=1 in mod 12. So, the question I propose, is:
For what a and b, does a have a (multiplicative) inverse mod b?
This tricky question will be the subject of this blog and the finale blog as well! Anyway, for now let’s just try to find a pattern in the multiplication tables, then apply that to inverses!
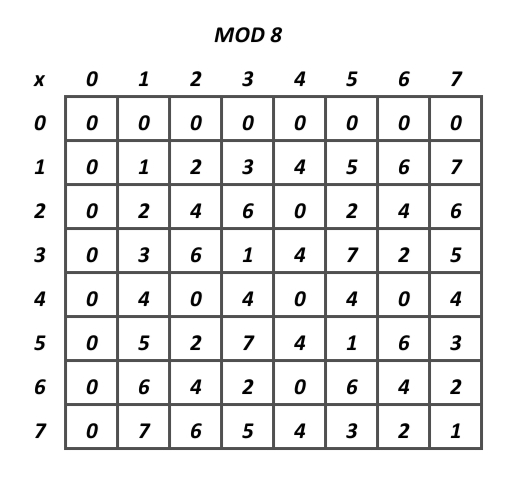
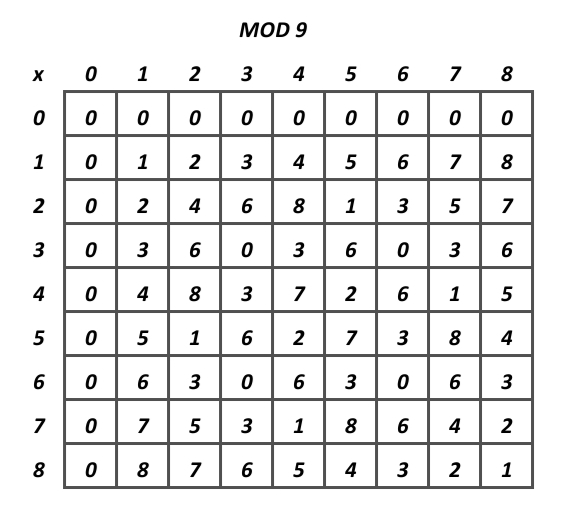
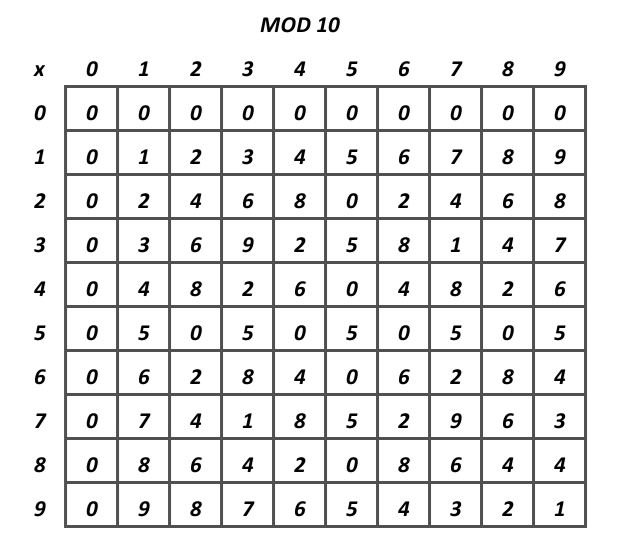
Ok, now what do multiplication tables have to do with modular arithmetic? Well, if we want to find whether or not maybe 7 has an inverse mod 9, we look at the 7 row, and if there is a 1 in that row, it has an inverse mod 9! In this case it does, since there is a 1 in the 7 column. Also, if you look closely at that row, it contains each number from 0-9 exactly once. If you look at any of the other grids, you might notice that in the rows that contain a 1, they also contain every other number exactly once. Also, look at the 7 and 11 grids in particular. Each and every single row follows these properties, which is not true of any of the other mods we’ve looked at. What do 7 and 11 have that none of the other numbers don’t… They’re prime! Check mod 13, 5, 17, and any other prime, it works for them all! We’ll worry about proving this in the finale, but for now, let’s end it off with a thought that might allow you to predict the final statement which we will prove in part 5! That thought is… A definition!
Relatively Prime: Two numbers a and b, are prime, iff they share no factors other than 1. In other words:
GCD(a,b)=1
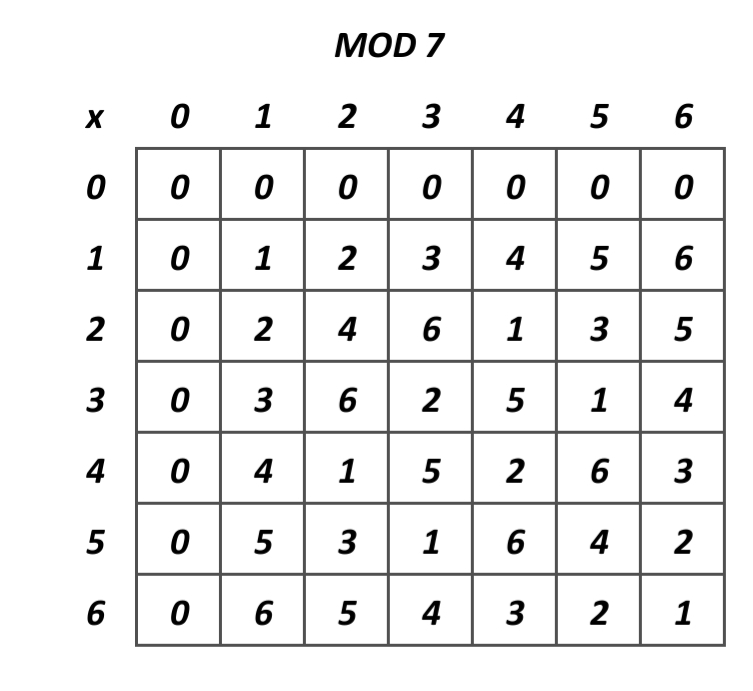
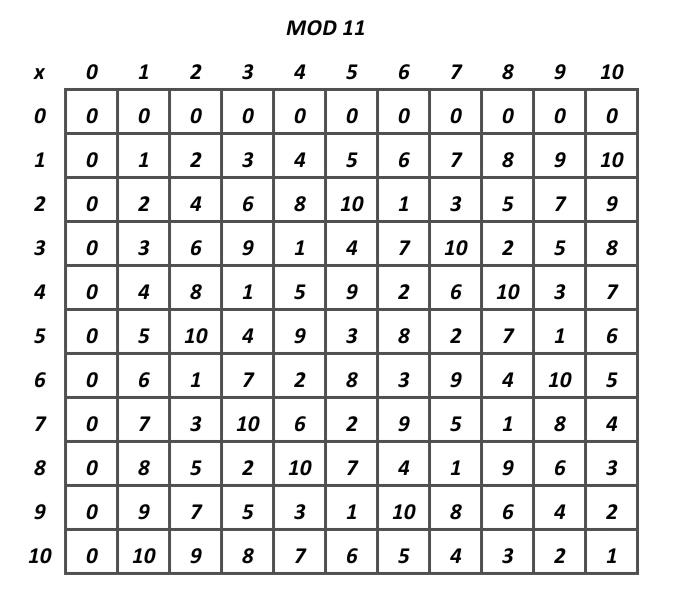
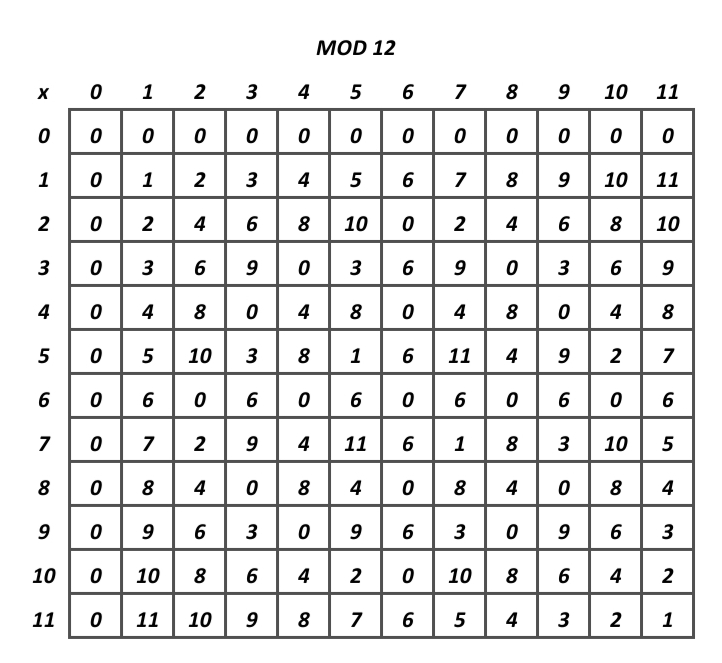
Love it! You did an awesome job explaining the multiplicative inverse in modular arithmetic. I suspect two typos. One is in the times table of mod 7 , 2*3=”6″. The other is the definition of relatively prime, I guess you mean GCD(a,b)=1 instead of LCM.
And also 3*3=9≡2 mod 7, but the table shows 3*3≡1 mod 7.
Thank you, all fixed!
Part 5?
When will you release Part 5?
Should be sometime tommorow, sorry I have been sick, so I haven’t been able to do much work on it.