Hi everyone! Today I am going to talk about the Fibonacci sequence and where it appears in nature.
Who is Fibonacci?
Leonardo Fibonacci (1175 – 1250) was a Pisan mathematician. Our numeral system is pretty conventional today, but in the 13th century, it was groundbreaking to the European world. So, in 1202, Fibonacci wrote a book called Liber Abaci which brought the Hindu-Arabic numerals to Europe. Inside the Liber Abaci was a problem involving rabbits. Imagine 1 pair of rabbits (one male, one female). The rabbit problem needs these “criteria”.
- No rabbits die.
- The female rabbit reproduces at the start of the third month, not the second.
- Every baby pair after that reproduces every two months as well.
How many pairs exist at the end of the year? Let us see a chart.
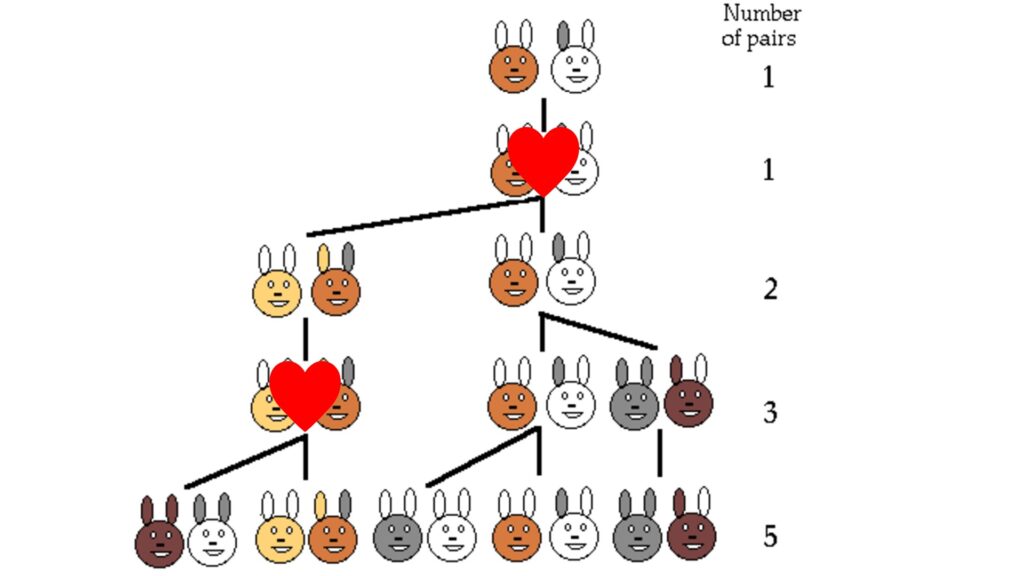
The first pair takes two months to breed, with the baby pair being born in the third month. Then, at the start of the fourth month, the original pair have again bred, but the baby pair born in the third month are still adults. Then, in month 5, the original pair has bred, the month 3 pair bred, and the month 4 pair bred, giving us 5 pairs. Eventually, we will get the sequence \(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,\cdots\) That is the Fibonacci sequence! After 1 year, we will have \(F_{12} = 144\) pairs (yes, that is how you write Fibonacci numbers). Let us focus on some more properties. Even though Fibonacci was not the first to discover this sequence (Indian mathematicians had discovered it over a millennium before Fibonacci), it was named after him.
\(F_{12}\) is special because \(F_{12}=12^2=144\). Also, the ratio of \(\dfrac{F_n}{F_{n-1}}\) trends to the golden ratio, written as \(\phi\), \(\varphi\), or simply Phi. (Fibonacci never made the connection between Phi and his sequence; the Holy Roman-German mathematician Johannes Kepler did.)
Now, what about nature? The spirals of pineapples, pine cones, sunflowers, and so on are the Fibonacci numbers! Even the petals of flowers! A clover usually has 3 leaves, and 3 is a Fibonacci number! 4-leaf clovers are rare because 4 is not a Fibonacci number.
Join me next time in Part 2 of the “Phi-Series” where we look into the Golden Ratio!
You should make an article about a closed form for the Fibonacci sequence!